a2+b2 formula in Pythagorean Theorem

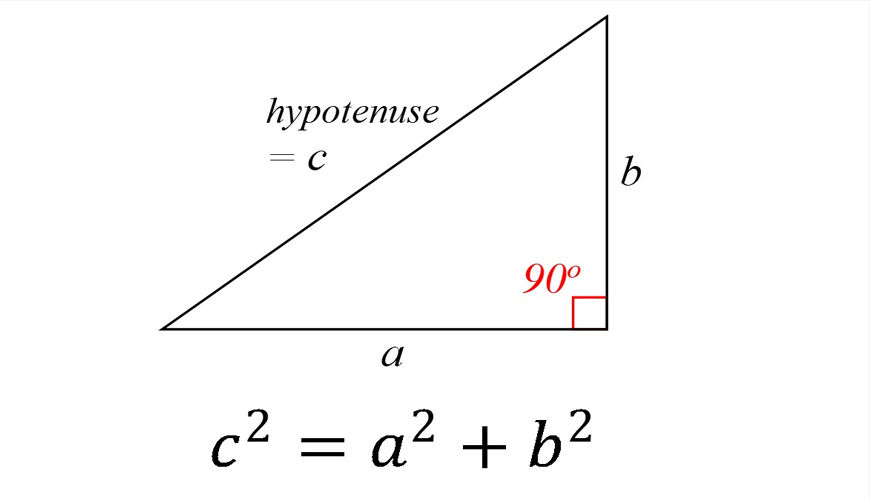
The formula a2+b2 is typically associated with the Pythagorean theorem in mathematics, which states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed as:

a^2 + b^2 = c^2

where:

• $c$ is the length of the hypotenuse,
• $a$ and $b$ are the lengths of the other two sides.

This theorem is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It is used in various calculations and can be applied in different contexts, from basic geometry to more advanced mathematics and physics.

a2+b2 Formula

The formula �2+�2a2+b2, especially in the context of the Pythagorean theorem, has a wide range of applications and implications in various fields.

Geometry and Trigonometry

• Right-Angled Triangles: The most direct application is in calculating the lengths of sides in right-angled triangles. If two sides are known, the third can be calculated.
• Trigonometric Identities: The theorem is foundational in trigonometry, leading to identities like sin2θ+cos2θ=1 when the sides are normalized to the hypotenuse.

Algebra

• Algebraic Proof: The theorem can be proven algebraically, offering insights into geometric properties via algebra.
• Generalization: The concept extends to more complex forms like the Euclidean distance formula in higher dimensions, d^2=x^2+y^2+z^2+….

Physics

• Vector Analysis: In physics, it’s used to calculate the magnitude of vectors in two-dimensional space.
• Analyzing Forces: For resolving forces or velocities into perpendicular components.

Engineering and Architecture

• Structural Design: Ensuring right angles in construction and design.
• Computer Graphics: Calculating distances and angles for rendering images and animations.

Mathematics Beyond Geometry

• Complex Numbers: The representation of complex numbers and their magnitudes involves a form of the Pythagorean theorem.
• Hilbert Spaces: In higher mathematics, it extends to abstract spaces, like Hilbert spaces in quantum mechanics.

Real-World Applications

• Navigation and Surveying: Calculating distances and plotting courses using map coordinates.
• Astronomy: Determining distances to nearby stars through parallax.

Historical Significance

• Ancient Mathematics: It’s one of the earliest known mathematical theorems, with evidence of knowledge in ancient civilizations like Babylon and Egypt.
• Philosophical Implications: It played a crucial role in the development of Greek mathematics and philosophy.

Must Read:

• Decrypting Digital Value: Bitcoins Key to Financial Transformation
• हनुमान चालीसा आरती | पढ़ने मात्र से बने बिगड़े काम

In summary, a2+b2 formula as part of the Pythagorean theorem is a cornerstone concept in mathematics with vast applications in various scientific and engineering fields. Its simplicity in form belies its broad utility and fundamental nature in understanding the world around us.