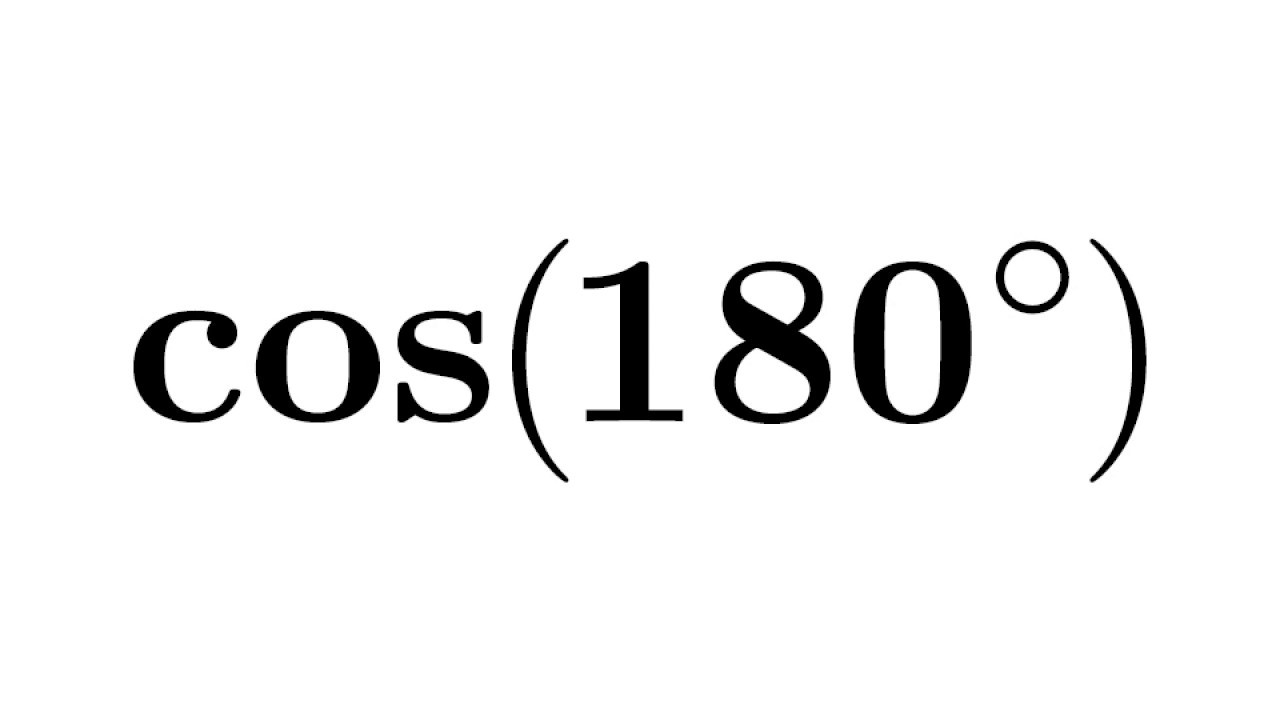Cos 180 Degree. The cosine function, denoted as cos(θ), is one of the six fundamental trigonometric functions used to relate the angles of a right triangle to the ratios of its sides. In a right-angled triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. The cosine function is periodic, oscillating between values of -1 and 1 as the angle varies. It is an essential concept in trigonometry, used extensively in mathematics, physics, engineering, and various other fields.
Table of Contents
Understanding Cos 180
Cos 180 refers to evaluating the cosine function at an angle of 180 degrees. The value of cos(180°) is -1. This means that the adjacent side’s length is negative relative to the hypotenuse in a right triangle with a 180-degree angle. Cos 180 is unique as it represents the horizontal component of a vector with a 180-degree direction in complex concept the Cartesian plane. The understanding of Cos 180 is vital in trigonometry and lays the groundwork for more cs in the subject.
Applications of Cos 180 in Trigonometry
The concept of Cos 180 finds applications in various trigonometric problems and real-world scenarios. One of the key applications is in understanding reflections and rotations. When an object is rotated by 180 degrees, the cosine function helps determine the resulting position of its points. Moreover, Cos 180 is crucial in analyzing periodic functions, such as waveforms and oscillations. This is especially relevant in fields such as signal processing and music theory.
Trigonometric Ratios and Cos 180
In trigonometry, the ratios of the sides of a right triangle with respect to its angles are called trigonometric ratios. Cos 180 is one of these ratios, and it represents the relationship between the adjacent side and the hypotenuse in a right triangle with a 180-degree angle. The trigonometric ratios, including Cos 180, are used extensively to solve problems involving angles, distances, and heights. They play a fundamental role in various branches of mathematics, such as geometry and calculus.
The Unit Circle and Cos 180
The unit circle is a fundamental tool used to relate angles to coordinates in the Cartesian plane. At 180 degrees, the cosine function reaches its lowest point, which is represented as (-1, 0) on the unit circle. This point is important in understanding the periodic nature of the cosine function. The unit circle is not only crucial for visualizing trigonometric functions but also has widespread applications in physics, engineering, and computer graphics.
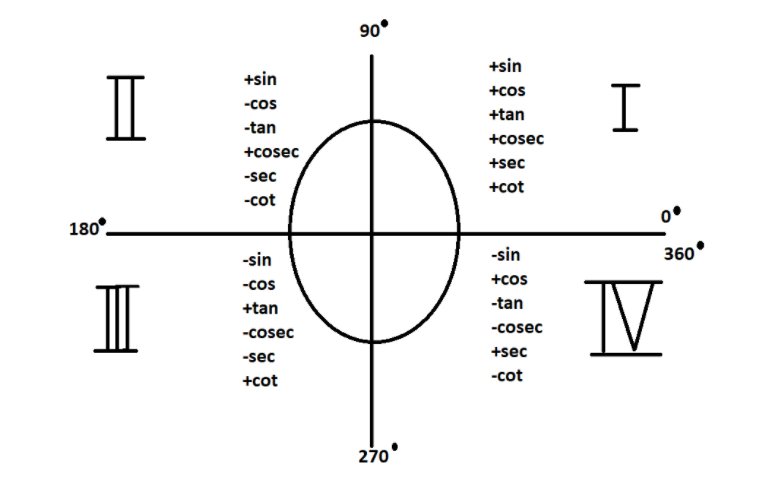
Graphical Representation of Cos 180
Graphing the cosine function for different angles creates a cosine curve, which is a periodic wave. At an angle of 180 degrees, the cosine curve reaches its minimum value, -1. The graphical representation of Cos 180 allows us to visualize its behavior and understand how it changes for various angles. The cosine curve has numerous applications in fields like sound waves, vibrations, and harmonic motion.
Evaluating Cos 180 in Degrees and Radians
Angles can be measured in degrees or radians, and it is essential to understand the conversion between these units. When evaluating Cos 180, it is important to note that the value remains the same, whether the angle is expressed in degrees or radians. Cos 180 in radians is also equal to -1. This conversion is crucial when working with trigonometric functions in calculus and advanced mathematical applications.
Cos 180 in Real-life Scenarios
Cos 180 finds practical applications in numerous real-life scenarios. For instance, it is employed in analyzing sound waves, where a 180-degree phase shift can lead to constructive or destructive interference. Understanding the behavior of Cos 180 is also important in navigation and astronomy, where it is used to determine positions and distances. Additionally, in mechanical engineering, understanding Cos 180 helps determine the positions of rotating components, such as gears and shafts.
Cos 180 in Physics and Engineering
In physics and engineering, Cos 180 is used to solve a wide range of problems. In physics, it is used in analyzing oscillatory motion, where an object oscillates back and forth through its equilibrium position. Cos 180 is also crucial in calculating work done against gravitational forces, which is essential in designing structures and mechanisms. In engineering, Cos 180 is often used in designing motion systems, robotics, and electrical circuits.
Cos 180 in Mathematics and Calculus
In mathematics, the cosine function appears in various mathematical concepts and calculations. In calculus, it is used in integration and differentiation, playing a fundamental role in solving differential equations and analyzing functions. Understanding the properties of Cos 180 is significant in solving complex mathematical problems, especially those involving trigonometric functions.
Other Trigonometric Functions Related to Cos 180
Cos 180 is related to other trigonometric functions, such as sine and tangent. The relationship between these functions can be expressed using identities, which provide shortcuts and simplifications when solving trigonometric equations. For example, the Pythagorean trigonometric identity allows us to relate the values of sine and cosine for any given angle.
Importance of Understanding Cos 180
Understanding Cos 180 is not merely an academic exercise. It has profound implications in various scientific and engineering disciplines. It forms the foundation for grasping more advanced trigonometric concepts and their applications in the real world. Moreover, a strong understanding of Cos 180 is essential for success in fields like physics, engineering, surveying, and architecture.
Common Mistakes and Misconceptions about Cos 180
Students often make common mistakes and harbor misconceptions when dealing with Cos 180. One common misconception is confusing the value of Cos 180 with Cos 0. Another mistake is assuming that Cos 180 is positive, similar to Cosine values for acute angles. Addressing these misconceptions can lead to a deeper understanding of trigonometry and improve problem-solving skills.
Tips for Solving Problems Involving Cos 180
To excel in trigonometry and related fields, developing effective problem-solving techniques for Cos 180 is crucial. Here are some valuable tips to approach and solve problems involving Cos 180 and other trigonometric functions:
- Identify the given angle and its context in the problem.
- Determine whether the angle is in degrees or radians, and convert if necessary.
- Use the definition of the cosine function to find the ratio of the adjacent side to the hypotenuse.
- Apply any relevant trigonometric identities or formulas to simplify the problem.
- Check the final result and ensure it makes sense in the given context.
Also Read:
Conclusion
Cos 180, with a value of -1, plays a critical role in trigonometry, mathematics, and various scientific and engineering disciplines. Its applications extend to real-life scenarios, where it helps analyze waveforms, rotations, and oscillations. Understanding Cos 180 enhances our ability to solve complex problems and provides us with valuable insights into the behavior of angles and periodic functions. This fundamental trigonometric function is a powerful tool in understanding the world around us and is indispensable in numerous applications across different fields.