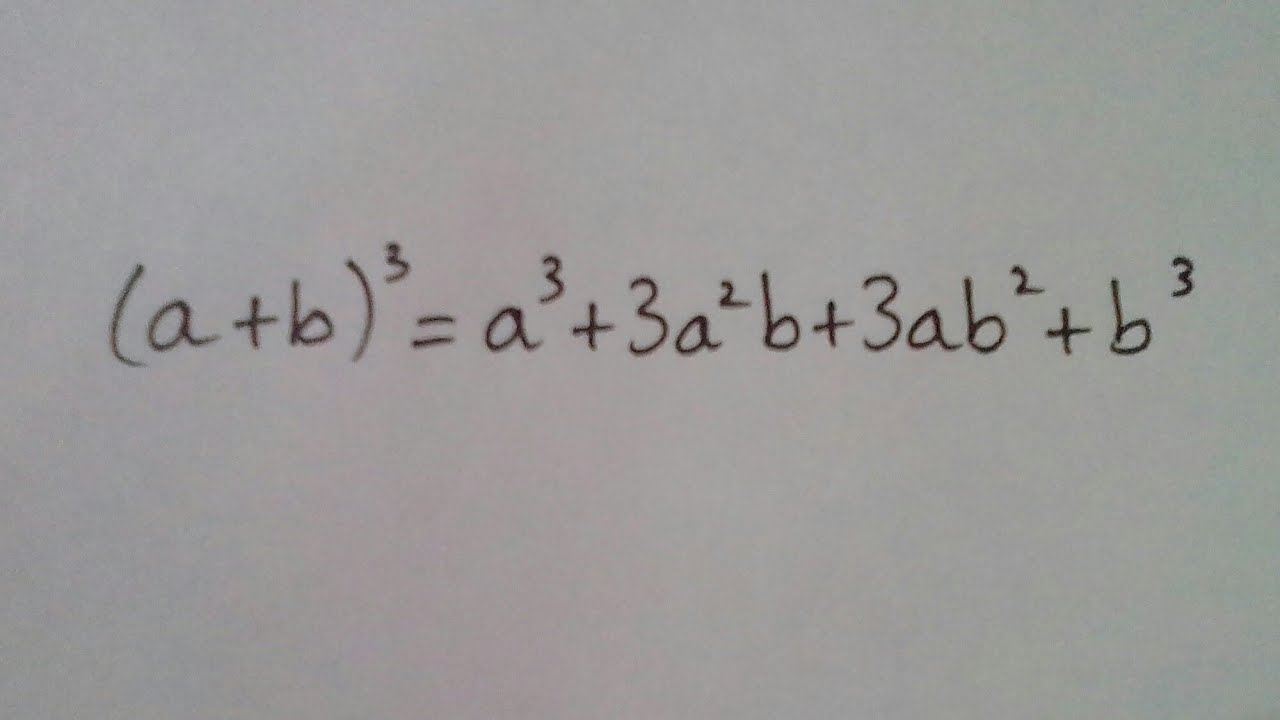In the vast landscape of mathematics, certain formulas stand out as powerful tools that have far-reaching applications. Among these, the (a+b)^3 formula holds a special place. This article is dedicated to unraveling the mysteries and applications of this intriguing formula. By the time you finish reading, you’ll have a deep understanding of how (a+b)^3 works and how it can be applied in various mathematical contexts.
Table of Contents
Understanding the Basics (a+b)^3 Formula
Before we plunge into the intricacies of the (a+b)^3 formula, let’s establish a solid foundation by grasping the fundamental concepts.
What is the (a+b)^3 Formula?
The (a+b)^3 formula represents an algebraic expression that encapsulates the cube of a binomial. In simpler terms, it provides a concise way to express the expansion of (a+b) raised to the third power.
Intriguingly, this formula is not just a mathematical curiosity but a versatile tool that finds relevance in numerous branches of mathematics and beyond.
The Expanded Form
Expanding the (a+b)^3 expression can appear daunting at first glance, but let’s break it down into manageable steps.
Step 1: Squaring the Binomial
Our journey begins by squaring the binomial (a+b) not once, but twice, resulting in the following expression:
(a+b)(a+b)(a+b)
Step 2: Expanding the Squares
The next step involves expanding these squared binomials individually. It’s crucial to remember that (a+b)(a+b) is equivalent to a^2 + 2ab + b^2. Therefore, our expression now looks like this:
(a^2 + 2ab + b^2)(a+b)
Step 3: Distributing
Now, it’s time to distribute the terms within the first set of parentheses across the second set:
a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3
Step 4: Combine Like Terms
In the final step of expansion, we simplify the expression by combining like terms:
a^3 + 3a^2b + 3ab^2 + b^3
This is the expanded form of (a+b)^3. By breaking it down step by step, we demystify what might initially seem like a complex process.
Applications in Mathematics and Beyond
Now that we’ve mastered the expansion, let’s explore the diverse applications of the (a+b)^3 formula.
Algebraic Simplification
In the realm of algebra, this formula shines as a tool for simplifying intricate expressions and equations. It enables mathematicians to condense complex relationships into more manageable forms, facilitating further analysis and problem-solving.
Calculus and Derivatives
Calculus, the study of rates of change and accumulation, frequently calls upon the (a+b)^3 formula. It plays a pivotal role in differentiation, allowing mathematicians to find derivatives of functions that involve binomial terms. The formula simplifies these calculations, making them more accessible and efficient.
Engineering and Physics
Engineers and physicists aren’t immune to the charm of (a+b)^3. In their world, this formula becomes a valuable asset when dealing with quantities that change dynamically over time. It assists in modeling and solving complex systems and equations, ensuring the structural integrity of bridges, buildings, and the success of experiments.
Must Read: DAG 101: A Beginners Guide to Innovative Cryptocurrency
Real-World Relevance
While mathematical formulas can often appear abstract, the (a+b)^3 formula holds tangible applications in the real world, which affect our daily lives.
Financial Forecasting
In the financial sector, analysts employ mathematical models that incorporate the (a+b)^3 formula to make predictions about future trends. By estimating growth rates and investment returns, they assist individuals and businesses in making informed financial decisions.
Structural Engineering
Structural engineers depend on the (a+b)^3 formula to calculate stress and strain on materials. By doing so, they ensure the safety and durability of buildings, bridges, and other critical infrastructure. This formula plays a pivotal role in designing structures that can withstand various environmental challenges.
Conclusion
In summary, the (a+b)^3 formula transcends its mathematical origins to become a powerful tool with applications in multiple fields. Whether you’re a mathematician, scientist, engineer, or financial analyst, understanding this formula’s versatility can significantly enhance your problem-solving abilities and contribute to innovative solutions in your respective domains.